7-2. Harrow-Hassidim-Lloyd (HHL) アルゴリズム¶
この節では、量子位相推定アルゴリズムの重要な応用先の一つであるHarrow-Hassidim-Lloyd (HHL) アルゴリズムについて紹介する。HHLアルゴリズムは(sparseな)連立一次方程式を高速に “解く” アルゴリズムであり、連立一次方程式は電磁気・熱流体解析や機械学習などあらゆる科学技術計算で用いられるために、非常に注目されている。 本節の内容は、原論文[1]およびレビュー論文[2]に基づいている。
問題設定¶
HHLアルゴリズムは、sparse (疎)で正則な \(N \times N\) 行列 \(A\) と \(N\) 次元のベクトル \(\bf{b}\) について、連立一次方程式 \(A\mathbf{x}=\mathbf{b}\)の解 \(\mathbf{x}=A^{-1}\mathbf{b}\) を効率的に「計算」するアルゴリズムである(この節では、ベクトルを 太字 で表す):
この式の意味について説明しよう。まず、ケットの中にベクトルが入った \(|\mathbf{x}\rangle, |\mathbf{b}\rangle\) といった状態は、以下のように定義されている:
ここで \(x_i, b_i\) はベクトルの \(i=0,1,\ldots, N-1\) 番目の成分であり、\(|i\rangle\) は\(i\)の2進数表示に対応する計算基底である(例えば、\(|5\rangle = |0\cdots0101\rangle\))。 \(N\) 成分のベクトルを表すのには、 \(\log_2 N\) 個の量子ビットを用意すればよい。 HHLアルゴリズムは、量子位相推定アルゴリズムと補助ビットを駆使して、 入力状態 \(|\mathbf{b}\rangle\) から解状態 \(| A^{-1}\mathbf{b} \rangle\) を精度よく高速に作り出すアルゴリズムなのである。
計算量の詳しい説明はこの節の最後に行うが、HHLアルゴリズムは上記の変換を\(O(\text{poly}(\log N))\)、つまり\(\log N\) の多項式程度の計算量で行うことができる。同様の計算を行う現在のベストな古典アルゴリズムの計算量は\(O(N)\)であるから、HHLアルゴリズムは指数加速を達成している。 ただしいくつかの重要な注意点がある:
行列 \(A\) は、sparseでなければならない。具体的には、各行に含まれる非ゼロの成分の数が \(O(\text{poly}(\log N))\) でなければならない。
与えられた古典データ \(\mathbf{b}\) から、量子コンピュータ上に状態 \(|\mathbf{b}\rangle\) を用意するのは一般には簡単でなく、愚直に入力すると \(O(N)\) の計算量がかかってしまう。上記の \(O(\text{poly}(\log N))\) という計算量は 状態 \(|\mathbf{b}\rangle\) が用意できた前提での話である。 コラム:量子ランダムアクセスメモリ (qRAM)では、この点をもう少し深く解説する。
出力された解状態 \(| A^{-1}\mathbf{b} \rangle\) を古典ベクトル \(A^{-1}\mathbf{b}\) として読みだすのも、愚直に行うと\(O(N)\) の時間がかかってしまい、指数加速が相殺されてしまう。
アルゴリズムの流れ¶
それでは、一番簡単なバージョンを例にとり、HHLアルゴリズムの流れを説明する。全体の回路図は次のとおりである[2]。 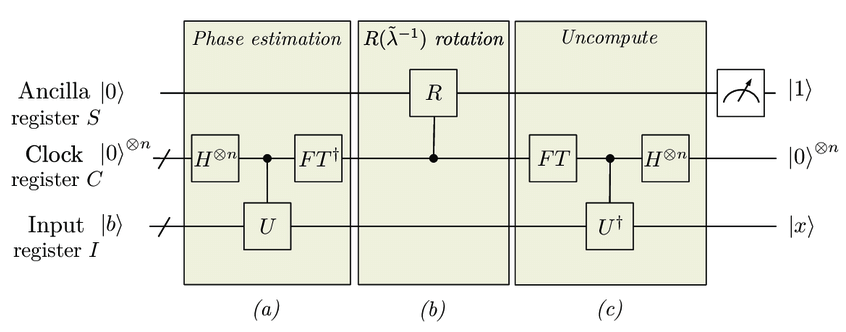
以下では簡単のため、 \(A\) はエルミート行列であると仮定する。Aがエルミートでないときは、
とおいて、解 \(\tilde{\mathbf{x}} = (\mathbf{0}, \mathbf{x})^T\) を用いれば良い。また、 \(A\)を適当に定数倍して、 \(A\) の固有値の最大値と最小値の差が \(2\pi\) 以下になるようにしておく(量子位相推定アルゴリズムを用いた時に固有値とビット列が1対1に対応するようにするため)。そして、その定数倍した \(A\) の固有値をシフトしたとき、全固有値が \([0, 2\pi]\) に収まるような定数シフト \(d\) も求めておく(詳細は後述する;とりあえず \(d=0\) としておく)。
1. 入力状態 \(|\mathbf{b}\rangle\) を用意する¶
先ほども述べたように、qRAMなどを使って、与えられた古典データ(ベクトル) \(\mathbf{b}\) から量子コンピュータ上に状態 \(|\mathbf{b}\rangle\) を用意する。 これから補助ビットを複数用いていくので、入力状態に用いる量子ビットには添字 \(I\) をつけて \(|\mathbf{b}\rangle_I\) と表記しておく。
2. ユニタリ演算 \(e^{i A }\) を用いた位相推定アルゴリズムを使って補助クロックビットに \(A\) の固有値を格納する¶
位相推定アルゴリズム用の補助クロック(C)ビットを \(n\) 量子ビット分用意する。
そして、ユニタリ演算 \(e^{iA}\) に対する量子位相推定アルゴリズムを実行し、\(A\) の固有値 \(\{ \lambda_i \}_{i=0}^{N-1}\)を補助クロックビットに格納する。 具体的に言うと、古典ベクトル \(\mathbf{b}\) を \(A\) の固有ベクトル \(\{\mathbf{u}_i \}_{i=0}^{N-1}\) で展開して
となっているとき、量子状態の意味でも
が成り立つことに注意すると、量子位相推定アルゴリズムによって
となることがいえる。ここで \(\tilde{\lambda}\) は \(\lambda\) の2進数表示 \(\lambda = 2\pi 0.j_1 \ldots j_n\) のビット列 \(j_1\ldots j_n\) である。
3. 補助クロックビットを用いた制御回転によって固有値の逆数をかける¶
さらに補助ビットを一個追加し、添字 \(S\) で表そう。
ここで、補助クロックビットを用いた次のような制御回転ゲートを作用させる。
つまり、補助クロックビットの値 \(\tilde{\lambda}\) に応じて、補助ビット \(S\) に 回転角 \(\theta = 2\arctan{( - c/(\lambda \sqrt{1-c^2/{\lambda}^{2} }) )}\) のY回転 \(R_Y(\theta)=e^{i\theta/2Y}\) を行うゲートを作用させる。 \(c\) はこのような制御回転ゲートを可能にするために導入した規格化定数であり、ありうる \(|\lambda|\) の最小値より小さくとっておけば良い: \(|c| \leq \max |\lambda|\)。なお、最初に定義した定数シフト \(d\) が非ゼロの時は、\(\lambda\) と \(\lambda + d\) と置き換えておけばよい。
この制御回転ゲートの構成はかなりテクニカルなので、興味ある読者は以下の注を読んでほしいが、かなりたくさんの補助ビットが必要になることをremarkしておく。
注:制御回転ゲートの構成法¶
量子回路は古典回路を包含するので、原理的には古典回路によって行えるどのような演算も行うことができる。そこで、回転角を計算する\(\lambda \to 2\arctan( - c/(\lambda \sqrt{1-c^2/\lambda^2}) )\) という古典演算を重ね合わせた \(|\lambda \rangle \to |2\arctan( - c/(\lambda \sqrt{1-c^2/\lambda^2}) ) \rangle\) というゲートも構成可能である。ただし、古典回路でNANDなどの不可逆なゲートが1つ出てくるたびに補助ビットが1つ以上必要であり、この算数を行うためだけにかなりの補助ビットが必要とされる。 そして、\(\theta\) の値に応じた制御回転ゲート \(|\theta\rangle |0\rangle_S \to |\theta\rangle R_Y(\theta) |0\rangle_S\) は量子位相推定アルゴリズムのように単純な制御 \(R_Y\) ゲート \(\Lambda(R_Y)\) を用いることで実装可能だから、所望の補助クロックビットを用いた制御回転ゲートも実装可能である。
4. 量子位相推定の逆演算を行い、補助クロックビットを元に戻す¶
制御回転によって、全体の状態は次のようになっている。
ここに量子位相推定アルゴリズムの逆演算を施すと、
となる。
5. 補助ビット \(S\) を測定する¶
最後に、補助ビット \(S\) を測定する。 1 が得られたとすると、状態は
となる。補助クロックビットも \(|0\cdots0\rangle\) に射影測定してしまえば、状態
が得られる。実はこれが \(| A^{-1}\mathbf{b} \rangle\) になっているのである!
\(\because\) \(A\) の固有値・固有ベクトルが \(\lambda_i, \mathbf{u}_i\) なので、 \(A = \sum_i \lambda_i \mathbf{u}_i {\mathbf{u}_i}^{\dagger}\) と固有値分解できる( \(\dagger\) は転置共役)。よって \(A^{-1} = \sum_i (\lambda_i)^{-1} \mathbf{u}_i {\mathbf{u}_i}^{\dagger}\) であり、 \(A^{-1}\mathbf{b} = \sum_i \beta_i (\lambda_i)^{-1} \mathbf{u}_i\) となる。規格化係数を適当に調整すれば、上記の状態が \(| A^{-1}\mathbf{b} \rangle\) となっていることが分かる。
計算量について¶
以上がHHLアルゴリズムの流れである。最後に計算量について触れておく。
\(s\) を \(A\) の sparsity、つまり各行に入っている非ゼロ要素の個数の最大値
\(\kappa\) を \(A\) の条件数: \(\kappa = |\lambda|_{\textrm{max}} / |\lambda|_{\textrm{min}}\) (固有値の絶対値の最大値と最小値の比)
\(\epsilon\) を出力状態の \(| A^{-1}\bf{b} \rangle\) からの誤差
とすると、現在最も効率的な HHL アルゴリズムでの計算量は、\(O(s \kappa \, \textrm{poly} (\log (s\kappa/\epsilon)) )\) である事が知られている[3]。 \(s=O(\textrm{poly}(\log N))\) と仮定していたので、仮に \(N\) だけに着目すると全体も \(O(\textrm{poly}(\log N))\) となる。 一方、古典アルゴリズムのベストの共役勾配法では計算量は \(O(Ns\kappa \log(1/\epsilon))\) なので[2]、HHL アルゴリズムは行列の次元 \(N\) について指数加速を実現している。
しかし、冒頭でも述べたように、この計算量は入力状態 \(|\mathbf{b}\rangle\) が用意できたと仮定した上での結果であり、出力 \(|A^{-1} \mathbf{b} \rangle\) をどう読み出せば良いかも考慮していない。 この入出力のオーバーヘッドに \(O(N)\) の時間がかかってしまった場合、上記の指数加速が相殺されてしまうので、HHLアルゴリズムは例えば \(\mathbf{x}\) のサンプリングを行うだけで実用上役に立つ、といった状況で用いるべきだと考えられる。