8-2. Grover’s algorithm

Some of the circuits here are constructed with a controlled_on setting. This is the multi-controlled gate experimental feature that has not yet been released as of quri_parts 0.17.0.

Grover’s algorithm is a quantum algorithm for searching for specific data from an unsorted database [1]. Grover’s algorithm can find a solution in \(O(\sqrt{N})\) queries (calling an oracle) for \(N\) unsorted data. Since \(O(N)\) queries are required for a classical computer, a quadratic acceleration is achieved by using a quantum algorithm.

Once the oracle is constructed, Grover’s algorithm can accelerate the entire search portion of any classical algorithm. For example

• Satisfiability problem (SAT problem)

• The problem of finding the original value from a particular hash value

and the latter has actually been proposed in a paper as a Bitcoin mining acceleration [2].

In this section, we first provide a theoretical explanation of Grover’s algorithm and then present an example implementation using QURI Parts.

Algorithm Flow

The flow of Grover’s algorithm is simple and is as follows. As in the previous section, consider the problem of searching for \(M\) solutions from a database of \(N\) elements, where the element labels are \(N\) digit bit sequences \(x = x_1 \ldots x_n\).

1. prepare a superposition of all states \(|s\rangle = \frac{1}{\sqrt{N}}\sum_x |x\rangle\).

2. apply oracle \(U_w\) (reversal operation on the solution)

3. apply the inversion operation \(U_s\) with \(|s\rangle\) as the axis of symmetry

4. Repeat steps 2 and 3 \(k\) times

5. perform the measurement

Let’s look at each step in detail.

1. prepare a superposition state of all states \(|s\rangle = \frac{1}{\sqrt{N}}\sum_x |x\rangle\).

This is easy. For the initial state \(|0\cdots0\rangle\), we can apply Hadamard gate \(H\) to all qubits.

\[(H\otimes \cdots \otimes H) |0\cdots0\rangle = \frac{1}{(\sqrt{2})^n} (|0\rangle+|1\rangle) \otimes \cdots \otimes (|0\rangle+|1\rangle) = |s\rangle\]

2. Apply the oracle \(U_w\) (reversal operation on the solution)

Next, we let the oracle act on the state \(|s\rangle\). Here, as an oracle, we will consider the operation “if \(x\) is a solution to the input \(|x\rangle\), the phase is inverted by multiplying by (-1), and if it is not a solution, nothing is done” as described at the end of previous section, and the auxiliary bits are omitted. In other words, define the oracle \(U_w\) as follows.

\[U_w = I - 2\sum_{w\in \text{solution}}|w\rangle \langle w|,\]

\[\begin{split} U_w|x\rangle = \begin{cases} |x\rangle \:\: \text{(x is not solution)} \\ -|x\rangle \:\: \text{(x is solution)} \end{cases}\end{split}\]

The oracle \(U_w\) is called an “inversion operation on the solution” because it inverts the phase only when the input is a solution.

3. Applying the inversion operation \(U_s\) with \(|s\rangle\) as the axis of symmetry

In step 2, we considered the inversion operation on the solution, and in step 3, we will apply the inversion operation \(U_s\) with the superposition of all states \(|s\rangle\) as the axis of symmetry.

\[U_s = 2 |s\rangle \langle s| - I\]

This operator acts on input state \(|\psi\rangle = a|s\rangle + b|s_\perp\rangle\) (\(|s_\perp\rangle\) is a vector orthogonal to \(|s\rangle\))as follows

\[U_s|\psi\rangle = a |s\rangle - b|s_\perp\rangle\]

and inverts only the phase of the part proportional to \(|s_\perp\rangle\).

4. Repeat steps 2 and 3 \(k\) times

Repeat the above two inversion operations \(U_w\) and \(U_s\). As we will see later, approximately \(O(\sqrt{N/M})\) iterations are sufficient to obtain a solution with high enough probability in the next step: measurement. In other words, the number of times to call the oracle is \(O(\sqrt{N})\).

5. Take a measurement

After the steps up to this point, the state is \((U_s U_w)^k | s \rangle\). \(k\) is the number of iterations of steps 2 and 3. As described below, in fact, (absolute value of) the coefficient of the state \(|w\rangle\) corresponding to the solution \(w\) is very large in this state, so if we perform the measurement in the computational basis, we can obtain the solution \(w\) (bit string) with a high probability.

Roughly speaking, this is the only operation to be performed in Grover’s algorithm, and it is very simple.

Geometric Explanation

Next, we provide a geometric explanation of why Grover’s algorithm works. (There are other explanations that focus on the average operation of the coefficients, see for example [3].)

Definition of a two-dimensional plane

First, consider a two-dimensional plane stretched in the following two states \(|\alpha\rangle,|\beta\rangle\).

\[|\alpha\rangle = \frac{1}{\sqrt{N-M}} \sum_{x \in {not solution}} |x\rangle\]

\[|\beta\rangle = \frac{1}{\sqrt{M}}\sum_{x \in solution} |x\rangle\]

The superposition state \(|s\rangle\) of all states can be expressed as follows, which shows that it is a vector in this 2-dimensional plane.

\[|s\rangle = \sqrt{\frac{N-M}{N}} |\alpha\rangle + \sqrt{\frac{M}{N}} |\beta\rangle\]

In particular, using angles which satisfies \(\cos{\frac{\theta}{2}} = \sqrt{\frac{N-M}{N}}, \sin{\frac{\theta}{2}} = \sqrt{\frac{M}{N}}\) we can write

\[|s\rangle = \cos{\frac{\theta}{2}} |\alpha\rangle + \sin{\frac{\theta}{2}} |\beta\rangle\]

This is illustrated in the following figure. (Note that since \(N \gg{} M\) in general in search problems, \(\sqrt{M/N}\) is close to 0 and \(\theta\) is often a positive number close to 0.)

Two inversion operations \(U_s U_w\) = rotation in a two-dimensional plane

Considering in this plane, the oracle \(U_w\) is an inversion operation with respect to the \(|\beta\rangle\) axis (\(U_w|\alpha\rangle =|\alpha\rangle, U_w|\beta\rangle = -|\beta\rangle\)). Therefore, after applying \(U_w\), applying inversion \(U_s\) with \(|s\rangle\) as the symmetry axis will result in a rotation in the \(|\alpha\rangle,|\beta\rangle\) plane by an angle \(\theta\). (see the figure).

Since Grover’s algorithm repeats \(U_s U_w\) \(k\) times, the state is rotated \(k\) times, and just before the measurement

\[(U_s U_w)^k |s\rangle = \cos{\frac{(2k+1)\theta}{2}} |\alpha\rangle + \sin{\frac{(2k+1)\theta}{2}} |\beta\rangle\]

When \(N \gg M\) , \(\theta\) was a positive number close to zero, so each time \(|s\rangle\) was acted on by \(U_s U_w\), the coefficient of \(|\alpha\rangle\) would decrease and that of \(|\beta\rangle\) would increase. Since \(|\beta\rangle\) was made up of a superposition of all solution states, this means that the probability of obtaining a solution increases when \((U_s U_w)^k |s\rangle\) is measured.

This is the reasons why Grover’s algorithm can successfully search for solutions.

Estimating the optimal \(k\).

Finally, let’s evaluate how much \(k\), the number of times to act on \(U_s U_w\), i.e., how many times to call the oracle. This will determine the computational complexity.

The closest \((U_s U_w)^k |s\rangle\) comes to \(|\beta\rangle\) is when \(\frac{(2k+1)\theta}{2}\) is close to \(\frac{\pi}{2}\), that is when \(k\) is

\[R = \text{ClosestInteger}\left( \frac{\pi}{2\theta} -\frac{1}{2} \right)\]

where \(\text{ClosestInteger}(\ldots)\) denotes the integer closest to \(\ldots\). Let us evaluate the upper bound of \(R\).

\[\frac{\theta}{2} \geq \sin \frac{\theta}{2} = \sqrt{\frac{M}{N}}\]

With the above equation that hold for \(\theta > 0\), we get

\[R \leq \left( \frac{\pi}{2\theta} -\frac{1}{2} \right) + 1 = \frac{\pi}{2\theta} + \frac{1}{2} \leq \frac{\pi}{4}\sqrt{\frac{N}{M}} + \frac{1}{2}\]

That is, \(R\) is at most \(O(\sqrt{N/M})\) and Grover’s algorithm works with \(O(\sqrt{N})\).

Example Implementation

Let us try to implement Grover’s algorithm using QURI Parts. (The implementation code is almost the same as in [4].)

from quri_parts.core.state import GeneralCircuitQuantumState
from quri_parts.qulacs.simulator import evaluate_state_to_vector
import matplotlib.pyplot as plt
## Function to plot the distribution of absolute values of coefficients
def show_distribution(
    state: GeneralCircuitQuantumState,
    n_qubits: int
):
    plt.bar(
        [i for i in range(pow(2, n_qubits))],
        abs(evaluate_state_to_vector(state).vector)
    )
    plt.show()

Checking the operation

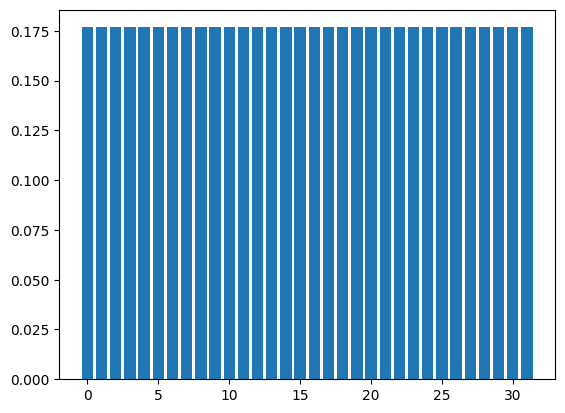
First, let’s implement Grover’s algorithm with 5 qubits and check its operation. The superposition state of all states \(|s\rangle\) can be created by acting on all bits of the state \(|0\cdots0\rangle\) with Hadamard gate.

from quri_parts.circuit import QuantumCircuit
from quri_parts.core.state import quantum_state

n_qubits = 5

def make_Hadamard(nqubits: int) -> QuantumCircuit:
    Hadamard = QuantumCircuit(nqubits)
    for i in range(nqubits):
        Hadamard.add_H_gate(i)
    return Hadamard


Hadamard = make_Hadamard(n_qubits)
state = quantum_state(n_qubits, circuit=Hadamard)

show_distribution(state, n_qubits)

Next, we create the oracle \(U_w\). Here we set \(|1\ldots1\rangle\) as the solution, and create an operator that adds a phase (-1) to only \(|1\ldots1\rangle\). Such an operator can be implemented as “an operator that apply the \(Z\) gate on the nqubitsth qubit when all qubits from the 0th to the nqubits-1th are 1.

import numpy as np

def make_U_w(n_qubits: int):
    U_w = QuantumCircuit(n_qubits)
    U_w.add_Z_gate(n_qubits-1, controlled_on={i: 1 for i in range(n_qubits-1)})
    return U_w

Uw = make_U_w(n_qubits)

Checking the action of the oracle, we can see that indeed only the last component (\(|1\cdots1\rangle\)) is inverted in phase.

from quri_parts.qulacs.simulator import evaluate_state_to_vector
state = quantum_state(n_qubits, circuit = make_Hadamard(n_qubits) + Uw)
print(evaluate_state_to_vector(state).vector)

[ 0.1767767+0.j  0.1767767+0.j  0.1767767+0.j  0.1767767+0.j
  0.1767767+0.j  0.1767767+0.j  0.1767767+0.j  0.1767767+0.j
  0.1767767+0.j  0.1767767+0.j  0.1767767+0.j  0.1767767+0.j
  0.1767767+0.j  0.1767767+0.j  0.1767767+0.j  0.1767767+0.j
  0.1767767+0.j  0.1767767+0.j  0.1767767+0.j  0.1767767+0.j
  0.1767767+0.j  0.1767767+0.j  0.1767767+0.j  0.1767767+0.j
  0.1767767+0.j  0.1767767+0.j  0.1767767+0.j  0.1767767+0.j
  0.1767767+0.j  0.1767767+0.j  0.1767767+0.j -0.1767767+0.j]

Similarly, create an inversion \(U_s\) with \(|s\rangle\) as the symmetry axis. Use the following equation holds.

\[U_s = 2 |s\rangle \langle s| - I = H^{\otimes n} (2 |0\cdots0\rangle \langle0\cdots0| - I) H^{\otimes n}\]

def make_U_s(n_qubits: int):
    Us = QuantumCircuit(n_qubits)
    for i in range(n_qubits):
        Us.add_H_gate(i)

    Us.add_RZ_gate(n_qubits-1, -2*np.pi)
    Us.add_X_gate(n_qubits-1)
    Us.add_Z_gate(n_qubits-1, controlled_on={i: 0 for i in range(n_qubits-1)})
    Us.add_X_gate(n_qubits-1)

    for i in range(n_qubits):
        Us.add_H_gate(i)

    return Us

Us = make_U_s(n_qubits)

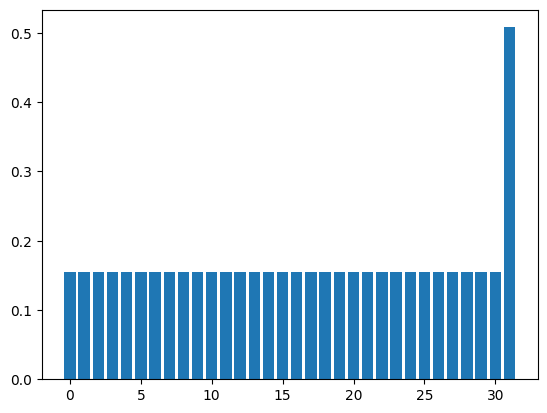
Now let’s apply \(U_s U_w\) just once and see how the probability distribution changes. The probability of all 1 states (the rightmost one) gets slightly larger.

from quri_parts.core.state import apply_circuit
## Prepare initial state
state = quantum_state(n_qubits, circuit=Hadamard)

## apply U_s U_w
state = apply_circuit(Uw + Us, state)
show_distribution(state, n_qubits)

Repeat this a few times and you’ll see.

## Create a solution state |1....1> to evaluate the inner product.
from quri_parts.core.state import ComputationalBasisState
target_state = quantum_state(n_qubits, bits=2**n_qubits-1)

## Run Grover's algorithm
state = quantum_state(n_qubits, circuit=Hadamard)

for i in range(4):
    state = apply_circuit(Uw, state)
    state = apply_circuit(Us, state)
    show_distribution(state, n_qubits)
    print(
        np.linalg.norm(
            evaluate_state_to_vector(state).vector.conj() @ evaluate_state_to_vector(target_state).vector
        )
    )

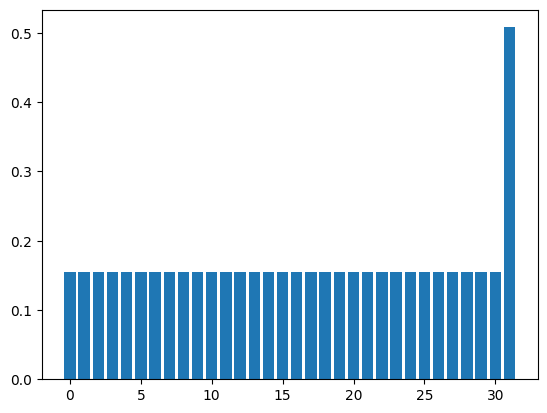
0.5082329989778305

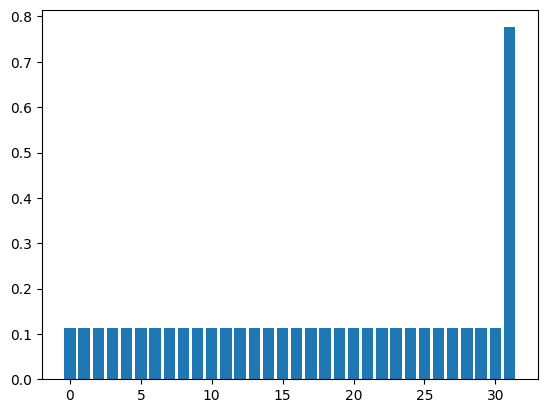
0.7761601777867947

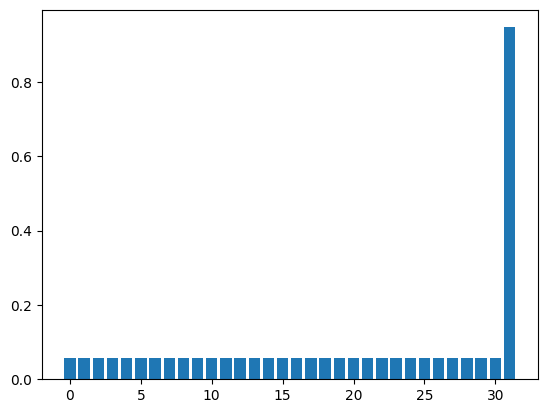
0.9470673343724091

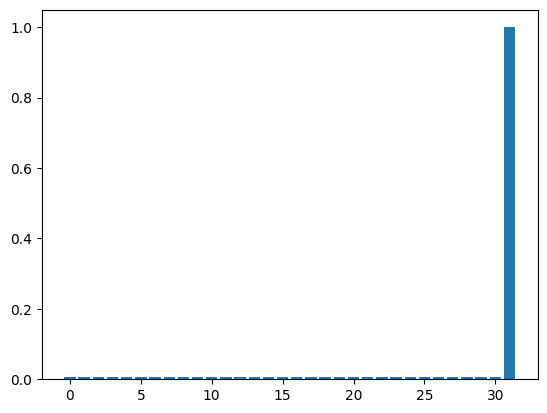
0.9995910741614723

After about \(k=4\) iterations, we got a solution state with probability almost 1. Let nqubits be a bit larger and check the behavior of the solution output probability for \(k\).

from quri_parts.core.state import ComputationalBasisState
n_qubits = 10
state = quantum_state(n_qubits)

## Create a solution state |1....1> to evaluate the inner product.
target_state = quantum_state(n_qubits, bits=2**n_qubits-1) ## 2**n_qubits-1 is binary number 1...1
target_state_vector = evaluate_state_to_vector(target_state).vector

## Run Grover's algorithm
Hadamard = make_Hadamard(n_qubits)
Uw = make_U_w(n_qubits)
Us = make_U_s(n_qubits)

result = []

state = quantum_state(n_qubits, circuit=Hadamard)
for k in range(30):
    state = apply_circuit(Uw, state)
    state = apply_circuit(Us, state)
    #show_distribution(state,nqubits)
    state_vector = evaluate_state_to_vector(state).vector
    result.append(
        np.linalg.norm(state_vector.conj() @ target_state_vector)
    )

max_k = np.argmax(result)
print( f"maximal probability {result[max_k]:5e} is obtained at k = {max_k+1}")

plt.plot(np.arange(1, 30+1), result, "o-")
plt.show()

maximal probability 9.997306e-01 is obtained at k = 25

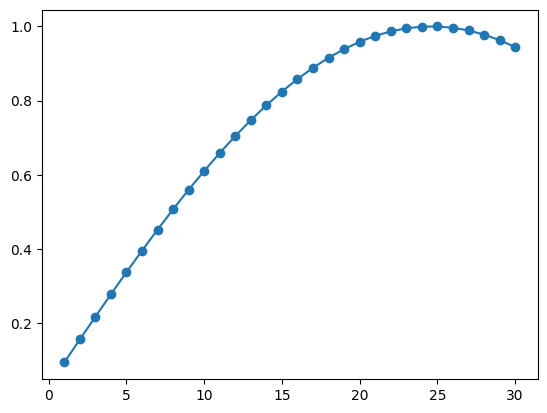
The target state is obtained with probability 1 almost \(k=25\) times. Also, the \(k\) dependence of the probability is a sine function, as we saw in the “Geometric Explanation” section.

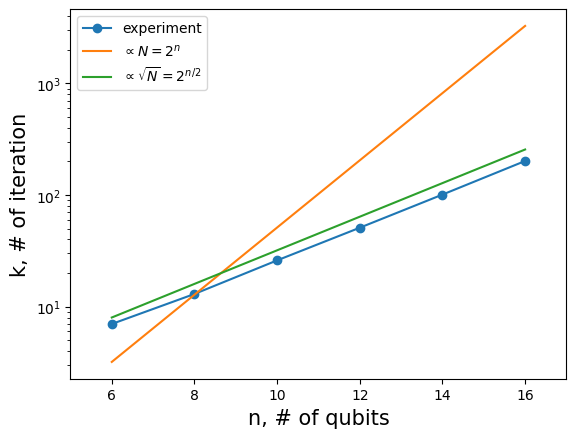
Finally, let’s see how the \(k\) needed to find the solution behaves with respect to the number of qubits.

result = []
min_nqubits = 6
max_nqubits = 16
for n_qubits in range(min_nqubits, max_nqubits+1, 2):
    ## Prepare circuit
    Hadamard = make_Hadamard(n_qubits)
    Uw = make_U_w(n_qubits)
    Us = make_U_s(n_qubits)

    ## Create a solution state |1....1> to evaluate the inner product.
    target_state = quantum_state(n_qubits, bits=2**n_qubits-1) ## 2**n_qubits-1 is binary number 1...1
    target_state_vector = evaluate_state_to_vector(target_state).vector

    state = quantum_state(n_qubits, circuit=Hadamard)

    ## Multiply U_s U_w until the probability starts to decrease
    tmp = 0
    flag = 0
    num_iter = 0
    while flag == 0 and num_iter <= 1000:
        num_iter += 1
        state = apply_circuit(Uw, state)
        state = apply_circuit(Us, state)
        state_vector = evaluate_state_to_vector(state).vector

        suc_prob = np.linalg.norm(state_vector.conj() @ target_state_vector)

        if tmp < suc_prob:
            tmp = suc_prob
        else:
            flag = 1
    result.append( [n_qubits, num_iter, suc_prob] )
    print(f"nqubits={n_qubits}, num_iter={num_iter}, suc_prob={suc_prob:5e}")

nqubits=6, num_iter=7, suc_prob=9.526013e-01
nqubits=8, num_iter=13, suc_prob=9.930691e-01
nqubits=10, num_iter=26, suc_prob=9.963280e-01
nqubits=12, num_iter=51, suc_prob=9.992534e-01
nqubits=14, num_iter=101, suc_prob=9.998851e-01
nqubits=16, num_iter=202, suc_prob=9.999368e-01

result_array = np.array(result)

plt.xlim(min_nqubits-1, max_nqubits+1)
plt.xlabel("n, # of qubits", fontsize=15)
plt.ylabel("k, # of iteration", fontsize=15)
plt.semilogy(result_array[:,0], result_array[:,1], "o-", label="experiment")
plt.semilogy(result_array[:,0], 0.05*2**result_array[:,0], "-", label=r"$\propto N=2^n$")
plt.semilogy(result_array[:,0], 2**(0.5*result_array[:,0]), "-", label=r"$\propto \sqrt{N}=2^{n/2}$")
plt.legend(fontsize=10)

<matplotlib.legend.Legend at 0x124b6f880>